Автор: Поздеев Андрей
При разработке электронных устройств на микроконтроллерах (далее МК) иногда возникает необходимость фильтровать тот или иной поток данных. Одним из часто встречающихся потоков данных являются данные с АЦП. Очевидно, что фильтровать сигнал в таких приложениях возможно, как до аналогово-цифрового преобразования, так и после. При широком спектре помех в сигнале необходимо применение фильтров высокого порядка в таких случаях рационально фильтровать сигнал после преобразования, возлагая на аналоговую часть масштабирование сигнала и предварительную фильтрацию с использованием пассивных RC фильтров первого порядка. Предварительная фильтрация нужна для ограничения ширины спектра преобразуемого сигнала.
В рамках данной статьи будет рассмотрен цифровой фильтр, уравнение которого в z виде имеет вид:
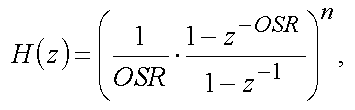 (1)
(1)
где OSR - количество выборок фильтра; n - порядок фильтра.
Далее мы увидим, что, не смотря на кажущуюся сложность, данный фильтр достаточно прост в реализации.
Для реализации фильтра в среде Simulink математического пакета MathLab уравнение (1) можно представить как произведение элементарных звеньев:
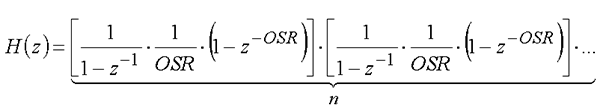 (2)
(2)
Звенья 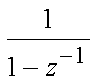 и
и 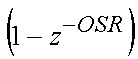 представляют собой цифровой интегратор и дифференциатор соответственно.
представляют собой цифровой интегратор и дифференциатор соответственно.
Математически цифровой интегратор может быть представлен в виде
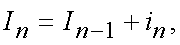 (3)
(3)
где In - текущий результат интегрирования; In-1 - результат интегрирования в предыдущем шаге; in - текущие значение потока данных.
Математически цифровой дифференциатор может быть представлен в виде
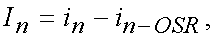 (4)
(4)
где In - текущий результат дифференцирования; in-OSR - значение в потоке OSR шагов назад; in - текущие значение потока данных
Тогда вариант реализации функциональной схемы фильтра второго порядка с числом выборок фильтра OSR=32 в среде Simulink будет иметь вид, приведенный на рис. 1:
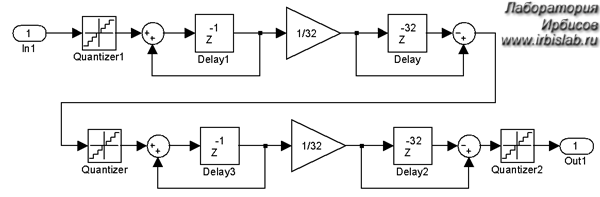
Рисунок 1 - Цифровой фильтр второго порядка в среде Simulink
Блоки Delay1, Delay3 и Delay, Delay2 формируют задержку 1 и 32 тактов соответственно, блоки Quantizer квантуют сигнал по уровню 1, т.е. входными и выходными значениями являются целые числа.
Реакция цифрового фильтра рис. 1 на ступенчатое изменение сигнала приведена на рис. 2:
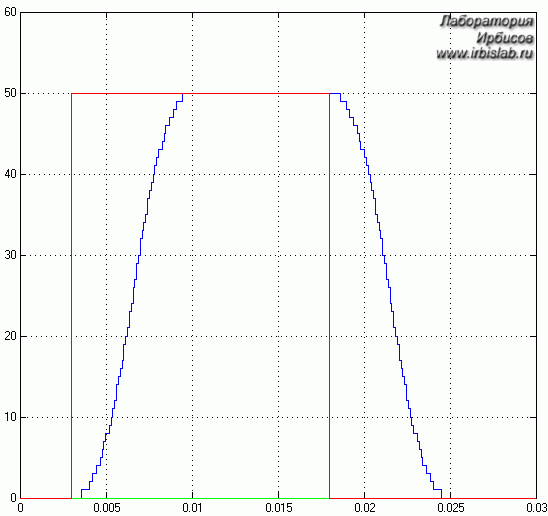
Рисунок 2 - Реакция цифрового фильтра второго порядка на ступенчатое изменение сигнала
Практическая реализация функциональной схемы фильтра рис. 1 представляет сложности, что связано с неизбежным насыщением интегратора. Для решения этой проблемы преобразуем уравнение (2) к виду:
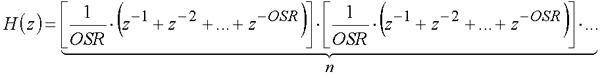 (5)
(5)
Функциональная схема в среде Simulink такого представления цифрового фильтра первого порядка с числом выборки OSR=16 приведена на рис. 3:
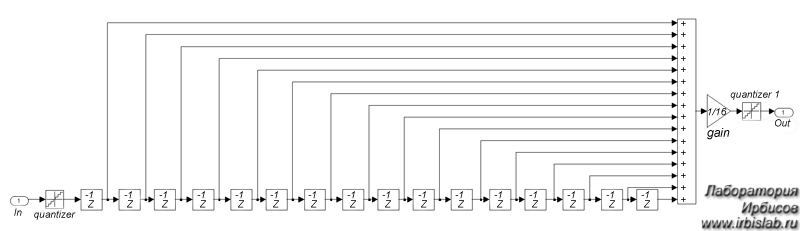
Рисунок 3 - Цифровой фильтр первого порядка
Таким образом, звено первого порядка рассматриваемого фильтра представляет собой среднее арифметическое значение последних OSR значений потока данных.
Вариант реализация уравнения (5) на языке Си приведен ниже:
#define FILTR_OSR 16
#define FILTR_ORDER 2
...
unsigned char FiltrData(unsigned char data)
{
static unsigned char bufFiltr[FILTR_ORDER][FILTR_OSR], nbufFiltr[FILTR_OSR];
unsigned int iFiltr[FILTR_ORDER];
unsigned char n, m;
for(m = 0; m < FILTR_ORDER; m++)
{
iFiltr[m] = 0;
for(n = 0; n < FILTR_OSR; n++)
{
iFiltr[m] += bufFiltr[m][n];
}
iFiltr[m] = iFiltr[m] / FILTR_OSR;
if(m == 0) {bufFiltr[m][nbufFiltr[m]] = data;}
else {bufFiltr[m][nbufFiltr[m]] = iFiltr[m-1];}
if(nbufFiltr[0] == FILTR_OSR) {nbufFiltr[m] = 0;}
else {nbufFiltr[m]++;}
}
return (unsigned char)iFiltr[(FILTR_ORDER - 1)];
}
Размер типа char в функции FiltrData 1 байт, тип int 2 байта. Переменные макросы FILTR_OSR и FILTR_ORDER определяют число выборок и порядок фильтра соответственно.
Из примера реализации видно, что повышение порядка фильтра не представляет сложности, однако необходимо учитывать производительность цифрового устройства, в котором применяется фильтр, чтобы время вычисления функции было меньше времени квантования аналогового сигнала. Кроме того необходимо учитывать объем резервируемой оперативной памяти т.к. массивы bufFiltr и nbufFiltr определенны с квалификатором static они сохраняют свое значение при последующем вызове и зарезервированная область не может использоваться другими функциями.
Объём резервируемой памяти в байтах определяется выражением:
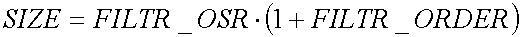 (6)
(6)
Для наглядности работы цифрового фильтра произведем моделирование его работы при подаче на его вход суммы постоянного сигнала значением 100 и случайной помехи частотой 1 кГц и амплитудой 10. Результат моделирования цифрового фильтра с числом выборок OSR = 32 и временем квантования 106 мкс приведен на рис. 4:
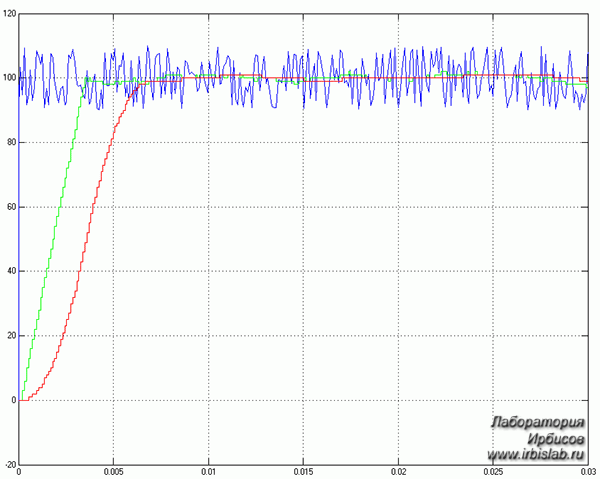
Рисунок 4 - Результат моделирования работы цифрового фильтра (Синий - входной сигнал; Зелёный - выход фильтра 1-го порядка; Красный - выход фильтра 2-го порядка)
Амплитудно-частная характеристика (далее АЧХ) цифрового фильтра, имеет вид:
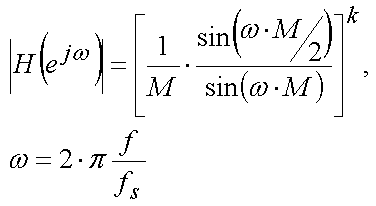 (7)
(7)
где M - число выборок фильтра OSR ; k - порядок фильтра; f - входная частота фильтра; fs - частота квантования по времени, величина обратная периоду квантования.
АЧХ цифрового фильтра с числом выборок OSR = 32 и временем квантования 106 мкс приведена на рис. 5, соответствующая логарифмическая частотная характеристика (далее ЛАЧХ) изображена на рис. 6. Частота на обоих графиках представлена в герцах.
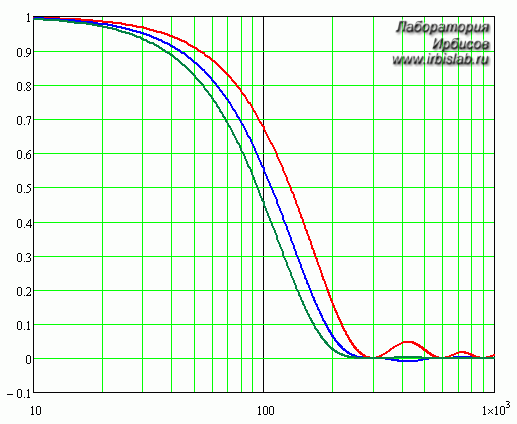
Рисунок 5 - АЧХ цифрового фильтра (Красный - 2-го порядка; Синий - 3-го порядка; Зелёный - 4-го порядка)
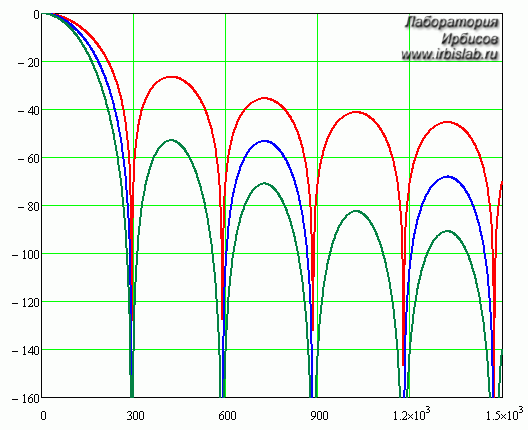
Рисунок 6 - ЛАЧХ цифрового фильтра (Красный - 2-го порядка; Синий - 3-го порядка; Зеленый - 4-го порядка)
Промоделируем работу цифрового фильтра применительно к достаточно распространенному МК ATmega8 фирмы ATMEL. Моделирование производилось в среде Proteus. Данные с АЦП передаем в функцию фильтра, а результат записываем в быстродействующий ЦАП. Схема приведена на рис. 7:
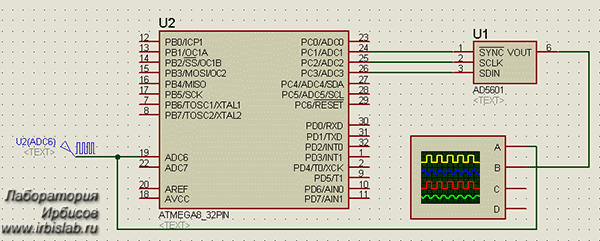
Рисунок 7 - Схема моделирования работы цифрового фильтра
Тактовая частота МК 8 МГц, период квантования с учетом задержки записи в ЦАП 235 мкс, фильтр 2-го порядка число выборок фильтра OSR = 16. Результат реакции фильтра на ступенчатое изменение сигнала приведен на рис. 8:
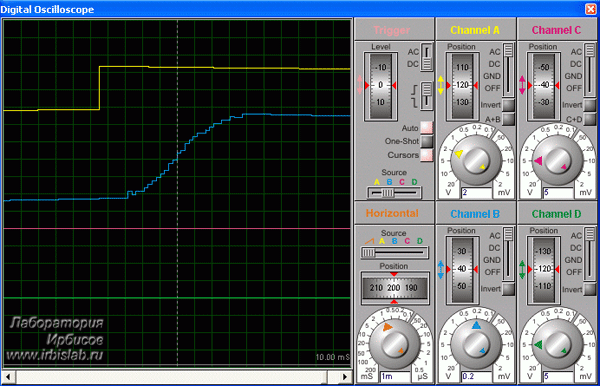
Рисунок 8 - Реакция цифрового фильтра 2-го порядка на ступенчатое изменение сигнала
Анализ полученных данных, в том числе и АЧХ, показывает, что рассмотренный цифровой фильтр обеспечивает высокое затухание, при отсутствии колебательности реакции на ступенчатое воздействие характерное для аналоговых фильтров. Рассмотренный фильтр может быть реализован даже на 8-ми разрядных микроконтроллерах с относительно низким быстродействием.
Данный фильтр рекомендуется применять для приложений, где требуется определение средней величины действующего значения сигнала, выделения его постоянной составляющей.
Обсуждение статьи на форуме
Copyright © Лаборатория Ирбиcов - Мягкой поступью к вершинам знаний и мастерства Все права защищены.
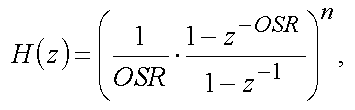 (1)
(1)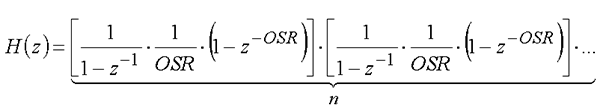 (2)
(2)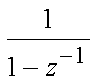 и
и 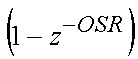 представляют собой цифровой интегратор и дифференциатор соответственно.
представляют собой цифровой интегратор и дифференциатор соответственно.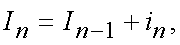 (3)
(3)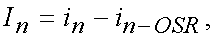 (4)
(4)

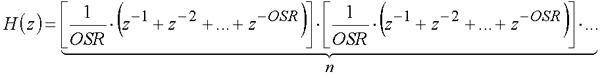 (5)
(5)
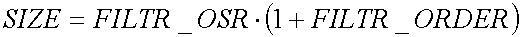 (6)
(6)
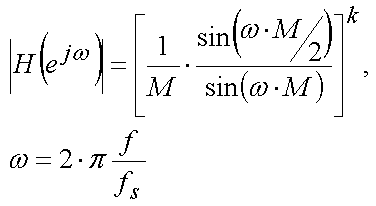 (7)
(7)


